Nettikasinon todennäköisyydet

Haluatko saada haltuusi menestyksen avaimet ja avata silmiesi eteen nettikasinon salaisuudet? Siinä tapauksessa voit iloita sen vuoksi, että maailmalla on rajattomasti mahdollisuuksia lyödä vetoja tai panostaa uhkapeleissä, joita on satoja ja jopa tuhansia. On kuitenkin kriittistä, että sinä henkilökohtaisesti ymmärrät nettikasino pelien todennäköisyydet, sillä muuten et voita juuri mitään netissä tai kivijalka kasinoilla, paitsi joskus tuurilla. Tästä johtuu uhkapelaamisen huono maine, sillä useimmat pelaajat odottavat heti voittavansa, vaikka he eivät edes ymmärrä miten peli toimii. Se on vähän sama kuin osallistuisi mäkihyppykilpailuihin ensimmäistä kertaa elämässään ja kuvittelisi heti voittavansa. Todennäköisesti tulet alas ja lujaa, joten on syytä opiskella suurella kärsivällisyydellä nettikasinon todennäköisyydet, jotta todellinen tienaaminen voi alkaa. Jotta voimme kasvattaa ymmärrystäsi tästä aiheesta, sinun on hyvä ensimmäiseksi tietää mikä on vedonlyöntikertoimien ja todennäköisyyksien todellinen merkitys, vai onko ne sinulle jo päivän selviä asioita? Jos ovat, käy suomalaiselle nettikasinolle pelaamaan, laita sata euroa tiskiin ja katso paljonko jää jäljelle. Jos eivät, lue eteenpäin ja opi tienaamaan satasellasi moninkertainen summa hetkessä.

Nettikasinon todennäköisyydet naurattavat tietämättömiä pelaajia, mutta vakavoittavat oikeat uhkapelaajat

Kun puhumme todennäköisyydestä silloin kun se liittyy uhkapelaamiseen, se voidaan määritellä seuraavasti: määrä tapoja voittaa jaettuna mahdollisten lopputulosten kokonaismäärällä. Todennäköisyyden ymmärtämisen juju on siinä, että sinulla pitää olla kyky erottaa riippumattomien ja riippuvaisten tapahtumien ero ja kummasta on kyse silloin kun puhutaan kasinopelaamisesta. Riippumattomat, eli itsenäiset tapahtumat ovat nimensä mukaisesti erillään muista tapahtumista. Tapahtumalla tarkoitamme tässä yhteydessä yhtä pelikierrosta. Yksittäinen itsenäinen pelikierros tarkoittaa siis sitä, että edellisten pelikierrosten ja tulevien pelikierrosten lopputulokset eivät vaikuta millään tavoin tämän kierroksen tulokseen. Tämä pätee usein moniin erilaisiin nettikasinon rahapeleihin, mutta harva pelaaja ymmärtää sitä. Paras esimerkki on kolikkopelit, sillä niiden kierrosten tulokset ovat täysin toisista kierroksista riippumattomia. Tämä on fakta, sillä satunnaislukugeneraattorin tärkein funktio on näyttää mahdollisimman satunnaisia lukuja ja jokainen kolikkopeli toimii generaattorin avulla. Pelaajat kuitenkin ajattelevat, että mitä kauemman he pelaavat, sitä lähempänä on suuri voitto. Tämän ajatuksen tapaisesti uskotaan myös, että jos monta tappiota on osunut putkeen, on pian aika voittaa. Myös käänteisesti ajatellaan, että voiton jälkeen ei voi tulla toista voittoa. Satunnaislukugeneraattori pitää kuitenkin huolen, että mikään näistä uskomuksista ei pidä paikkaansa. Tällaiset aatokset ovat hyvin laajalle levinneet ilman todellisuuspohjaa. Kolikkopelien todellisen luonteen vuoksi niiden pelaaminen on kuitenkin hauskaa, sillä jättipotti voi osua millä tahansa kierroksella.

Nettikasinon pelit, joiden tapahtumat ovat toisistaan riippuvaisia

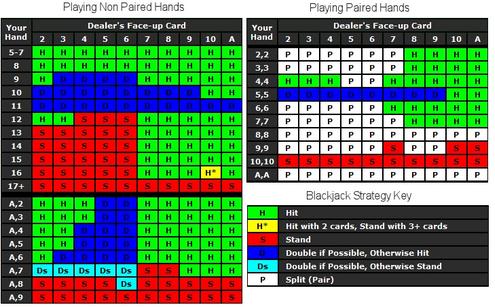
Edellä mainitut esimerkit käsittelivät tapahtumia, jotka ovat täysin itsenäisiä. On olemassa myös pelejä, joissa tapahtumat ovat jossain määrin toisistaan riippuvaisia. Se tarkoittaa sitä, että edellinen tapahtuma vaikuttaa seuraavaan jne. Yksi tällainen esimerkki on blackjack, jota pelataan yhdellä pakalla. Joka kerta kun pakasta poistetaan kortti, todennäköisyys samansuuruisen kortin osumiselle pienenee, sillä tällöin yksi neljästä kortista on poistettu jäljelle jäävästä pakasta. Näin ollen esimerkiksi rouvan vetämisen todennäköisyys on pelin alussa 4/52 tai 7,6 prosenttia. Jos rouva vedetään, seuraavan rouvan osumisen todennäköisyys on enää 3/51, eli 5,8 prosenttia. Vedonlyöntikertoimet vuorostaan tarkoittavat kertoimia, jotka voidaan määritellä vaikka tähän tapaan: tapahtuman todennäköisyys kaikkia muita tapahtumia vastaan poissulkien tapahtuma itse. Kun olet sisäistänyt tämän lausekkeen, olet valmis kovaan uhkapelaamiseen.